Question

A simple pendulum of mass 0.50 kg and length 0.75 m is held still and then released from an angle of 10° at t = 0. At what time does the pendulum first reach its maximum kinetic energy? (a) 0.43 s, (b) 0.53 s, (c) 1.1 s, (d) 1.7 s, (e) 3.4 s. AD string on a guitar is 648 mm long, has a mass of 1.92 g and a fundamental frequency of 147 Hz. How far from the end of the string is the fret associated with the G note, which has a frequency of 110 Hz? (a) 81.5 mm, (b) 163 mm, (c) 245 mm, (d) 326 mm, (e) 408 mm.

Answer 1

Step-by-step explanation:

The motion of the pendulum will be be SHM with time period equal to

T =
`2\pi\sqrt{(l)/(g) }`

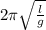
l = .75 m , g = 9.8

T =
`2\pi\sqrt{(.75)/(9.8) }`

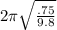
T = 1.73 s .

Time to reach the point of maximum velocity or maximum kinetic energy

= T /4

= 1.73 /4

= 0.43 s

For notes on Guitar , The formula is

n =
`(1)/(2l) \sqrt{(T)/(m) }`

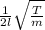
n is fequency of the note , T is tension of string , m is mass per unit length of string , l is length of string.

For fundamental note , l = .648 m and f = 147 Hz

147 =
`(1)/(2*.648) \sqrt{(T)/(m) }`

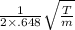
For G note

110 =
`(1)/(2* l) \sqrt{(T)/(m) }`

`(147)/(110) =(l)/(.648)`

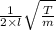
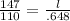
l = 866 mm

Distance from the end of string

866 - 648 = 218 mm or 245 mm

Option c ) is correct .