Question

Prove that if a and b are integers, then a^2-4b egal or non-egal 2

Answer 1

tex]a^2 - 4b \\eq 2[/tex]

Explanation:

We are given that a and b are integers, then we need to show that
`a^2 - 4b \\eq 2`

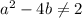
Let
`a^2 - 4b = 2`

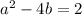
If a is an even integer, then it can be written as
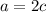`a = 2c`, then,

`a^2 - 4b = 2\\(2c)^2 - 4b =2\\4(c^2 -b) = 2\\(c^2 -b) =(1)/(2)`

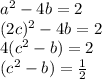
RHS is a fraction but LHS can never be a fraction, thus it is impossible.

If a is an odd integer, then it can be written as
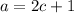`a = 2c+1`, then,

`a^2 - 4b = 2\\(2c+1)^2 - 4b =2\\4(c^2+c-b) = 2\\(c^2+c-b) =(1)/(4)`

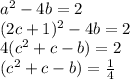
RHS is a fraction but LHS can never be a fraction, thus it is impossible.

Thus, our assumption was wrong and
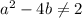`a^2 - 4b \\eq 2`.