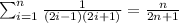Question

Prove that (from i=1 to n) sum([1/((2i-1)(2i+1))] = n/(2n+1). If true use induction, else give smallest value of n that it is false for.

Answer 1

The statement is true

Explanation:

We will prove by mathematical induction that, for every natural n,

`\sum^(n)_(i=1)(1)/((2i-1)(2i+1)) =(n)/(2n+1)`

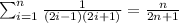
We will prove our base case, when n=1, to be true.

base case:

`\sum^(1)_(i=1)(1)/((2-1)(2+1)) =(1)/(3)=(n)/(2n+1)`

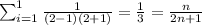
Inductive hypothesis:

`\sum^(n)_(i=1)(1)/((2i-1)(2i+1)) =(n)/(2n+1)`

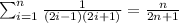
Now, we will assume the induction hypothesis and then uses this assumption, involving n, to prove the statement for n + 1.

Inductive step:

`\sum^(n+1)_(i=1)(1)/((2i-1)(2i+1)) =\sum^(n)_(i=1)(1)/((2i-1)(2i+1))+(1)/((2(n+1)-1)(2(n+1)+1))=(n)/(2n+1)+(1)/((2n+1)(2n+3))=(n(2n+3)+1)/((2n+1)(2n+3))=(2n^2+3n+1)/((2n+1)(2n+3))=((2n+1)(n+1))/((2n+1)(2n+3))=(n+1)/(2n+3)=(n+1)/(2(n+1)+1)`

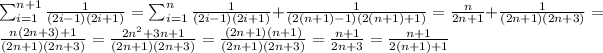
With this we have proved our statement to be true for n+1.

In conlusion, for every natural
`n`.

`\sum^(n)_(i=1)(1)/((2i-1)(2i+1)) =(n)/(2n+1)`