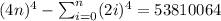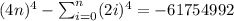Answer:
The statement is true for every n between 0 and 77 and it is false for

Step-by-step explanation:
First, observe that, for n=0 and n=1 the statement is true:
For n=0:
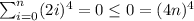
For n=1:
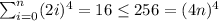
From this point we will assume that
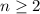
As we can see,
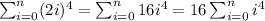 and
and
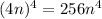 . Then,
. Then,
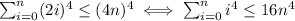
Now, we will use the formula for the sum of the first 4th powers:
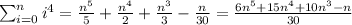
Therefore:
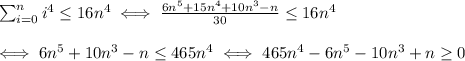
and, because
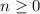 ,
,
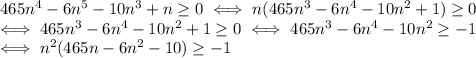
Observe that, because
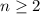 and is an integer,
and is an integer,
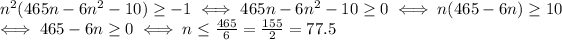
In concusion, the statement is true if and only if n is a non negative integer such that

So, 78 is the smallest value of n that does not satisfy the inequality.
Note: If you compute
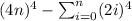 for 77 and 78 you will obtain:
for 77 and 78 you will obtain: