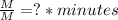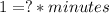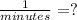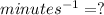Answer:
Units for parameter k would be
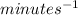 .
.
Explanation:
The concentration of CA0 is given in M (moles per liter), which is the unit for CA; if we show units inside parenthesis in the equation, it would be:

For the concentration units of CA0 not to be affected by the units of the factor (1-e-k*t), this factor would have to be a number without units.
Since 1 is a constant without units, for the constant e to be able to subtract from 1 it would have to be a number without units, which also applies to the factor k*t.
For the factor k*t to be a number without units, k must have units that can be canceled when multiplied by t, which is given in minutes, so k must have units of
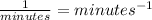
This can be confirmed by operating the equation using only its units (units of parameter k are noted by a question mark):