Question

A ball is thrown vertically upward with an initial speed of 30.0 m/s at a height of 1.5 m above the ground level. In the absence of air resistance, (a) how high does the ball go, (b) how much time does it take for the ball to reach its maximum height, and (c) what is the total time the ball is in the air before striking the ground?

Answer 1

Answer: Ok, this problems gives the next info:

Initial velocity = 30m/s

initial position = 15 m

So the only force in our problem is the gravitational, ence the acceleration will be:

a(t) = -9.8
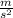`(m)/(s^(2) )` constant.

for the velocity we must integrate the acceleration over time, and add the integration constant, in this case the initial velocity.

we get v(t) = -9.8
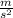`(m)/(s^(2) )`*t + 30m/s

for the position we integrate over time again, this time the integration constant will be the initial position.

x(t) =
`(9.8)/(2)`
`(m)/(s^(2) )`*
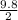
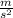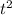`t^(2)`+ 30m/s*t + 1.5m

and start doing some resolutions.

(a) how high does the ball go

in this problem you need to obtain the time where the ball stops goin up and starts going down, and put that time in the position equation.

For this, we see v(t0) = 0 so t0 = 30/9.8 = 3.06s

then x(3.06) = 50 meters.

(b) how much time does it take for the ball to reach its maximum height.

Well, we already obtained it it, is 3.06 seconds.

(c) what is the total time the ball is in the air before striking the ground?

here you must see when x(t1) = 0, because if the position is zero, then it means that the ball striking the ground.

As the position is a quadratic function of the time, we must use the bashkara equation so t =
`\frac{-30 +- \sqrt{30^(2) +4*4.9*1.5}  }{-2*4.9}`

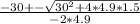
this gives us two times, we only took the positive one, because is the one that makes physical sense.

then t = 6.172 seconds.