Answer:
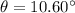
Step-by-step explanation:
Given that,
Magnetic field,
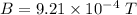
Acceleration of the electron,
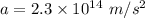
Speed of electron,

The force due to this acceleration is balanced by the magnetic force as :
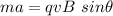
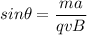
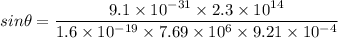
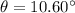
So, the angle between the electron's velocity and the magnetic field is 10.6 degrees. Hence, this is the required solution,