Answer:
Part A:
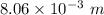
Part B:

Step-by-step explanation:
Given:
 = initial velocity of the electron =
= initial velocity of the electron =

 = electric field strength = 9100 N/C
= electric field strength = 9100 N/C
Assumptions:
 = mass of the electron =
= mass of the electron =
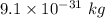
 = final velocity of the electron = 0 m/s
= final velocity of the electron = 0 m/s
 = distance at which the electron comes to rest
= distance at which the electron comes to rest
 = magnitude of charge on an electron =
= magnitude of charge on an electron =

 = taken by the electron to return to its initial position
= taken by the electron to return to its initial position
 = displacement of the electron
= displacement of the electron
Part A:
Since the electron moves in the direction of the electric field, the electric force will act on it in the direction opposite to electric field. This electric force does work on it to make the electron come to rest.
Using the work-energy theorem, the work done by the electric field will be equal to the kinetic energy change of the electron.
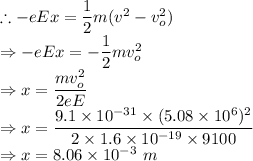
Hence, the electron comes to rest by travelling a distance of
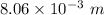 .
.
Part B:
In this part, let us first find out the acceleration of the electron due to the electric force.
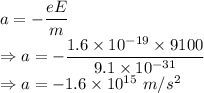
The electron moves with the above acceleration constantly as it moves in the uniform electric field.
Since the electron is supposed to move from a point and then again move back to the same point. This means the displacement of the electron is zero.
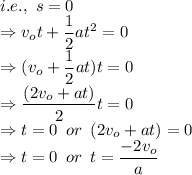
Since the electron starts moving at t = 0 s.
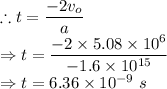
Hence, the electron returns to the starting position after
 .
.