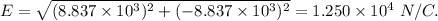Answer:

Step-by-step explanation:
Given:
- Charge on each corner of the square,
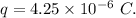
- Length of the side of the square,
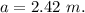
According to the Coulomb's law, the strength of the electric field at a point due to a charge
 at a point
at a point
 distance away is given by
distance away is given by
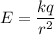
where,
 = Coulomb's constant =
= Coulomb's constant =
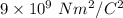 .
.
The direction of the electric field is along the line joining the point an d the charge.
The electric field at the point P due to charge at A is given by
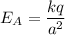
Since, this electric field is along positive x axis direction, therefore,
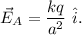
 is the unit vector along the positive x-axis direction.
is the unit vector along the positive x-axis direction.
The electric field at the point P due to charge at B is given by
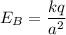
Since, this electric field is along negative y axis direction, therefore,

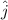 is the unit vector along the positive y-axis direction.
is the unit vector along the positive y-axis direction.
The electric field at the point P due to charge at C is given by
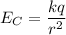
where,
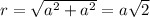 .
.
Since, this electric field is along the direction, which is making an angle of
 below the positive x-axis direction, therefore, the direction of this electric field is given by
below the positive x-axis direction, therefore, the direction of this electric field is given by
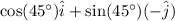 .
.
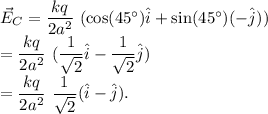
Thus, the total electric field at the point P is given by
![\vec E = \vec E_A+\vec E_B +\vec E_C\\=(kq)/(a^2)\hat i+(kq)/(a^2)(-\hat j)+(kq)/(2a^2)\ (1)/(\sqrt 2)(\hat i-\hat j).\\=\left ( (kq)/(a^2)+(kq)/(2\sqrt 2\ a^2) \right )\hat i+\left ((kq)/(a^2)+(kq)/(2\sqrt 2\ a^2) \right )(-\hat j)\\=(kq)/(a^2)\left [\left ( 1+(1)/(2\sqrt 2) \right )\hat i+\left (1+(1)/(2\sqrt 2) \right )(-\hat j)\right ]\\=(kq)/(a^2)(1.353\hat i-1.353\hat j)](https://img.qammunity.org/2020/formulas/physics/college/vo6ffdns7b2hvz914vm48o50w8cmq29q67.png)
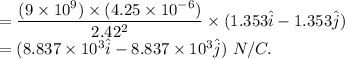
The magnitude of the electric field at the given point due to all the three charges is given by