Question

Look at sample problem 17.10 in the 8th edition Silberberg book.

The research and development unit of a chemical company is studying the reaction of methane and H2S, two components of natural gas:

CH4 (g) + 2 H2S (g) ⇋ CS2 (g) + 4 H2 (g)

In one experiment, 1.0 mol of CH4, 1.0 mol of CS2, 2.0 mol of H2S, and 2.0 mol of H2 are mixed in a 400. ml vessel at 960°C. At this temperature, Kc = 225.

In which direction will the reaction proceed to reach equilibrium? Enter right, left, or at equilibrium,

If the concentration of methane at equilibrium is 2.0 M, what is the equilibrium concentration of H2? Enter a number to 1 decimal places.

Answer 1

Answer : The reaction must shift to the product or right to be in equilibrium. The equilibrium concentration of
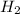`H_2` is 7.0 M

Explanation :

Reaction quotient (Qc) : It is defined as the measurement of the relative amounts of products and reactants present during a reaction at a particular time.

First we have to determine the concentration of
`CH_4,H_2S,CS_2\text{ and }H_2`.

`\text{Concentration of }CH_4=\frac{\text{Moles of }CH_4}{\text{Volume of solution}}=(1mol)/(400mL)* 1000=5M`

`\text{Concentration of }H_2S=\frac{\text{Moles of }H_2S}{\text{Volume of solution}}=(2mol)/(400mL)* 1000=2.5M`

`\text{Concentration of }CS_2=\frac{\text{Moles of }CS_2}{\text{Volume of solution}}=(1mol)/(400mL)* 1000=2.5M`

`\text{Concentration of }H_2=\frac{\text{Moles of }H_2}{\text{Volume of solution}}=(2mol)/(400mL)* 1000=5M`

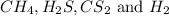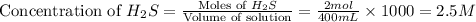
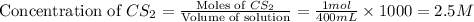
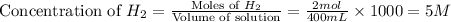
Now we have to determine the value of reaction quotient (Qc).

The given balanced chemical reaction is,

`CH_4(g)+2H_2S(g)\rightarrow CS_2(g)+4H_2(g)`

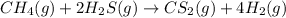
The expression for reaction quotient will be :

`Q_c=([CS_2][H_2]^4)/([CH_4][H_2S]^2)`

In this expression, only gaseous or aqueous states are includes and pure liquid or solid states are omitted.

Now put all the given values in this expression, we get

`Q_c=((2.5)* (5)^4)/((2.5)times (5)^2)=25`

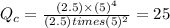
Equilibrium constant : It is defined as the equilibrium constant. It is defined as the ratio of concentration of products to the concentration of reactants.

There are 3 conditions:

When
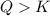`Q>K` that means product > reactant. So, the reaction is reactant favored.

When
`Q<K` that means reactant > product. So, the reaction is product favored.

When
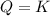`Q=K` that means product = reactant. So, the reaction is in equilibrium.

The given equilibrium constant value is,
`K_c=225`

From the above we conclude that, the
`Q<K` that means reactant > product. So, the reaction is product favored that means reaction must shift to the product or right to be in equilibrium.

Now we have to calculate the concentration of
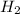`H_2` at equilibrium.

The given balanced chemical reaction is,

`CH_4(g)+2H_2S(g)\rightarrow CS_2(g)+4H_2(g)`

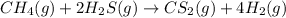
Initial conc. 2.5 5 2.5 5

At eqm. (2.5-x) (5-2x) (2.5+x) (5+4x)

The concentration of
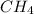`CH_4` at equilibrium = 2.0 M

As we know that, at equilibrium

(2.5-x) = 2.0 M

x = 0.5 M

The concentration of
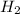`H_2` at equilibrium = (5+4x) = 5 + 4(0.5) = 7.0 M

Therefore, the equilibrium concentration of
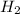`H_2` is 7.0 M