Answer:
for all values
Explanation:
u = (t - 2, 6 - t, - 4)
v = ( - 4, t - 2, 6 - t)
Angle between them, θ = 120°
Use the concept of dot product of two vectors
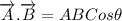
Magnitude of u =
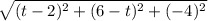
=
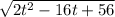
Magnitude of v =
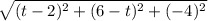
=
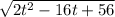

By the formula of dot product of two vectors
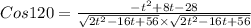

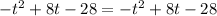
So, for all values of t the angle between these two vectors be 120.