Question

Two bicyclists, starting at the same place, are riding toward the same campground by different routes. One cyclist rides 1290 m due east and then turns due north and travels another 1410 m before reaching the campground. The second cyclist starts out by heading due north for 1890 m and then turns and heads directly toward the campground. (a) At the turning point, how far is the second cyclist from the campground? (b) In what direction (measured relative to due east within the range (-180˚, 180˚]) must the second cyclist head during the last part of the trip?

Answer 1

Answer: Ok, so we know that them start on the same place.

First, the first one rides 1290 to the east, and 1410 to the north.

So if we put the 0 at the place where they start, north is the Y axis and east the X axis, we could describe the campground is in (1290,1410)

a) when the second cyclist turns, he traveled 1890m to the north, se the point where he is, is described by (0, 1890). We want to know how far is from the campground which we already know that is located in (1290,1410), so if we subtract we get distance = (0,1890) - (1290,1410) = (-1290, 1890 - 1410) = (1290, 480). The total distance will be D =
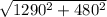`\sqrt{1290^(2) + 480^(2)  }` = 1376.4 meters.

b) You want to know in what angle should he turn now.

So again, the cyclist is on the point (0,1890) and the campground is on the point (1290,1410) so he want to go 1290 meters to east, and -480 meters to north. If we define this two amounts as the cathetus of triangle rectangle, the route that he must follow is the hypotenuse of said triangle.

So the angle that he must turn (counting from the east, or the +x axis, counterclockwise) is defined by Tg(A) = -480/1290 = -0.372.

A = aTg(-0.372) = -20° aprox.