Question

The population mean annual salary for environmental compliance specialists is about ​$62,000. A random sample of 32 specialists is drawn from this population. What is the probability that the mean salary of the sample is less than ​$59,000​? Assume σ=​$6,200.

Answer 1

Answer: 0.002718

Explanation:

Given : The population mean annual salary for environmental compliance specialists is about ​$62,000.

i.e.
`\mu=62000`

Sample size : n= 32

`\sigma=6200`

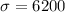
Let x be the random variable that represents the annual salary for environmental compliance specialists.

Using formula
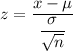`z=(x-\mu)/((\sigma)/(√(n)))`, the z-value corresponds to x= 59000 will be :

`z=(59000-62000)/((6200)/(√(32)))\approx(-3000)/((6200)/(5.6568))=-2.73716129032\approx-2.78`

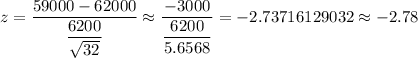
Now, by using the standard normal z-table , the probability that the mean salary of the sample is less than ​$59,000 :-

`P(z<-2.78)=0.002718`

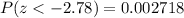
Hence, the probability that the mean salary of the sample is less than ​$59,000= 0.002718