Answer:
As consequence of the Taylor theorem with integral remainder we have that

If we ask that
 has continuous
has continuous
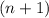 th derivative we can apply the mean value theorem for integrals. Then, there exists
th derivative we can apply the mean value theorem for integrals. Then, there exists
 between
between
 and
and
 such that
such that
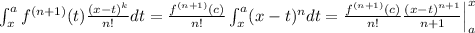
Hence,

Thus,

and the Taylor theorem with Lagrange remainder is
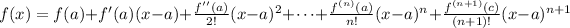 .
.
Explanation: