Answer:
Th magnitude of each Force will be

Step-by-step explanation:
Given:
- Length of each side of the equilateral triangle, L=1 m
- Magnitude of each point charge
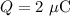
Since all the charges are identical and distance between them is same so magnitude of the force between each charge is equal.
Let F be the force between the particles. According to Coulombs Law we have

Now the the force on any charge by other two charges will be F and the angle between the two force is
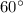
Let
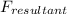 be the force on nay charge by other two
be the force on nay charge by other two
By using vector Law of addition we have

The angle made by the resultant vector will be
