Question

Assume that for a particular tire brand, the probability of wearing out before 30,000 miles is 0.25. For someone who buys a set of iour of these tires, what is the probability that all will last at least 30,000 miles? You be a suitable model in this case.

Answer 1

The probability that all will last at least 30,000 miles is 0.3164.

Explanation:

Consider the provided information.

For a particular tire brand, the probability of wearing out before 30,000 miles is 0.25. Someone who buys a set of four of these tires,

That means the probability of not wearing out is 1-0.25 = 0.75

Now use the binomial distribution formula.

`^nC_r (p^(n-r))(q^r)`

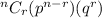
Substitute p = 0.25, q=0.75, r=4 and n=4

`^4C_4 (0.25)^(4-4)(0.75)^4`

`1 * 0.75^4`

`0.3164`

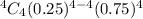
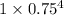
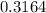
The probability that all will last at least 30,000 miles is 0.3164.