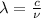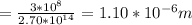Question

(a) The energy of photon incident on a material is 1.42 eV. ( Determine the minimum frequency of an incident photon that can interact with a valence electron and elevate the electron to become free. (ii) What is the corresponding wavelength? (b) Repeat part (a) for a photon energy of 1.12 eV.

Answer 1

a)

3.43*10^{14} Hz

8.75*10^{-7} m

b)

2.70*10^{14} Hz

1.10*10^{-6} m

Step-by-step explanation:

GIVEN DATA:

a)

i)we know that

E = h\\u

where E is energy

h = plank's constant = 6.625* 10^{-34} j-s

`\\u = frequency`

`\\u = (E)/(h) = (1.42*1.6*10^(-19) v)/(6.625*10^(-34))`

`\\u = 3.43*10^(14) Hz`

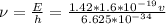
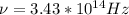
ii)wavelength is given as

`\lambda = (c)/(\\u)`

`= (3*10^8)/(3.43*10^(14)) = 8.75*10^(-7) m`

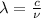
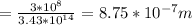
b) i) i)we know that

`E = h\\u`

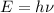
where E is energy

h = plank's constant = 6.625* 10^{-34} j-s

`\\u = frequency`

`\\u = (E)/(h) = (1.12*1.6*10^(-19) v)/(6.625*10^(-34))`

`\\u =2.70*10^(14) Hz`

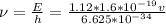
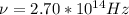
ii)wavelength is given as

`\lambda = (c)/(\\u)`

`= (3*10^8)/(2.70*10^(14)) = 1.10*10^(-6) m`