Answer:
The function is not injective.
The function is not surjective.
The function is not bijective.
Step-by-step explanation:
A function f(x) is injective if, and only if,
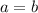 when
when
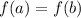 .
.
So
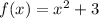
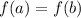
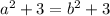
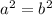
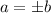
Since we may have
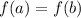 when, for example,
when, for example,
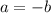 , the function is not injective.
, the function is not injective.
A function f(x) is surjective, if, and only if, for each value of y, there is a value of x such that
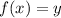 .
.
We have that y is composed of all the real numbers.
Here we have:
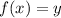
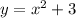
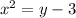
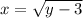
There is only a value of x such that
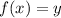 for
for
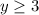 . So the function is not surjective.
. So the function is not surjective.
A function f(x) is bijective when it is both injective and surjective. So this function is not bijective.