Answer:
The initial population was approximatedly 3535 inhabitants.
Explanation:
The population of the city can be given by the following differential equation.
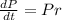 ,
,
In which r is the rate of growth of the population.
We can solve this diffential equation by the variable separation method.
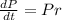
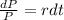
Integrating both sides:
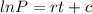
Since ln and the exponential are inverse operations, to write P in function of t, we apply ln to both sides.
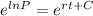
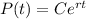
C is the initial population, so:
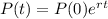
Now, we apply the problem's statements to first find the growth rate and then the initial population.
The problem states that:
In two years the population has doubled:
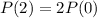
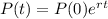

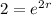
To isolate r, we apply ln both sides


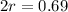
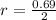
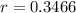
So
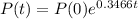
In two years the population has doubled and a year later there were 10,000 inhabitants.
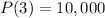
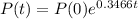
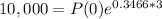
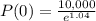

The initial population was approximatedly 3535 inhabitants.