Question

The maximum mass that can be hung verti from a string without breaking the string is TO KE. A length of this string that is 2 m long is used to rotate a 0.5 kg object in a circle on a frictionless table with the string horizontal. The maximum speed that the mass can attain under these conditions without the string breaking is most nearly (A) 5 m/s (B) 10 m/s (C) 14 m/s (D) 20 m/s (E) 100 m/s .: S

Answer 1

Step-by-step explanation:

The maximum mass that can be hung from a string, m = 10 kg

Length of the string, l = 2 m

Mass of the object, m = 0.5 kg

Let v is the maximum speed that the mass can attain under these conditions without the string breaking. If T is the maximum tension in the string. So,

`T_(max)=mg`

`T_(max)=10* 9.8=98\ N`

The centripetal force is provided by the tension in the string such that :

`T_(max)=(mv^2)/(r)`

`v=\sqrt{(T_(max)r)/(m)}`

`v=\sqrt{(98* 2)/(0.5)}`

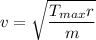
v = 19.79 m/s

or

v = 20 m/s

So, the maximum speed that the mass can attain under these conditions without the string breaking is 20 m/s. Hence, this is the required solution.