Question

Three negative point charges q1 =-5 nC, q2 = -2 nC and q3 = -5 nC lie along a vertical line. The charge q2 lies exactly between charge q1 and q3 which are 16 cm apart. Find the magnitude and direction of the electric field this combination of charges produces at a point P at a distance of 6 cm from the q2

Answer 1

Ep= 5450N/C in direction (-x)

Step-by-step explanation:

Conceptual analysis

The electric field at a point P due to a point charge is calculated as follows:

E = k*q/d²

E: Electric field in N/C

q: charge in Newtons (N)

k: electric constant in N*m²/C²

d: distance from charge q to point P in meters (m)

Equivalence

1nC= 10⁻⁹C

1cm= 10⁻²m

Graphic attached

The attached graph shows the field due to the charges q₁, q₂ y q₃ in the P (x=6, y=0):

As the charge q₁ ,q₂ , and q₃ are negative the field enter the charges.

E₁: Electric Field due to charge q₁.

E₂: Electric Field due to charge q₂.

E₃: Electric Field due to charge q₃.

Field calculation due to q₁ and q₃

Because q₁ = q₃ and d₁ = d₃, then, the magnitude of E₁ is equal to the magnitude of E₃

d₁=d₃=d

`d=\sqrt{6^(2)+8^(2)  } =10cm=0.1m`

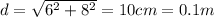
q₁=q₃= -5nC= 5*10⁻⁹C

E₁ = E₃= k*q/d² = 9*10⁹*5*10⁻⁹/0.1² = 4500 N/C

E₁x = E₃x= - 4500*(6/10)= -2700 N/C

E₁y = -4500*(8/10)= -3600 N/C

E₃y= +4500*(8/10)=+3600N/C

Field calculation due to q₂

E₂x= k*q₂/d₂²= -9*10⁹*2*10⁻⁹/0.6²= -50 N/C

Magnitude and direction of the electric field in the point P (Ep)

Epx= E₁x+ E₂x+E₃x = -2700 N/C-50 N/C-2700 N/C= -5450N/C

Epy= E₁y+ E₃y= -3600 N/C+3600N = 0

Ep= 5450N/C in direction (-x)