Question

There are 129 schools in the NCAA's Division 1 Football Bowl Subdivision. Of these, 115 have nicknames that end in "s" (like the UCLA Bruins) 19 have nicknames that involve a color (the Stanford Cardinal), and · 13 nicknames involve both a color and end in "s" (the California Golden Bears). How many teams have nicknames without a color and don't end in "s?

Answer 1

There are 8 teams that have nicknames without a color and don't end in "s.

Explanation:

This can be solved by treating each value as a set, and building the Venn Diagram of this.

-I am going to say that set A are the teams that have nicknames that end in S.

-Set B are those whose nicknames involve a color.

-Set C are those who have nicknames without a color and don't end in "s.

We have that:

`A = a + (A \cap B)`

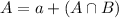
In which a are those that have nickname ending in "s", but no color, and
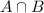`A \cap B` are those whose nickname involves a color and and in "s".

By the same logic, we have

`B = b + (A \cap B)`

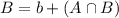
In which b are those that nicknames involves a color but does not end in s.

We have the following subsets:

`a,b, (A \cap B), C`

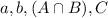
There are 129 schools, so:

`a + b + (A \cap B) + C = 129`

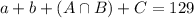
Lets find the values, starting from the intersection.

The problem states that:

13 nicknames involve both a color and end in "s". So:

`A \cap B = 13`

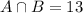
19 have nicknames that involve a color. So:

`B = 19`

`B = b + (A \cap B)`

`b + 13 = 19`

`b = 6`

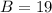
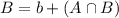
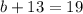
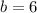
115 have nicknames that end in "s". So:

`A = 115`

`A = a + (A \cap B)`

`a + 13 = 115`

`a = 102`

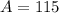
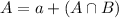
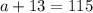
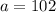
Now, we just have to find the value of C, in the following equation:

`a + b + (A \cap B) + C = 129`

`102 + 6 + 13 + C = 129`

`C = 129 - 121`

`C = 8`

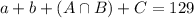
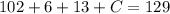
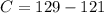
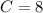
There are 8 teams that have nicknames without a color and don't end in "s.