Question

Question 8: A 150 mL of buffer contains 0.045 M carbonic acid (H2CO3) and 0.025 M sodium hydrogen carbonate (HCO3). If 3.0 mL of 0.15M HCl is added to the buffer, what is the new pH? pKa = 6.37

Answer 1

Answer: The new pH of resulting solution is 6.03

Step-by-step explanation:

We are adding hydrochloric acid to the solution, so it will react with salt (sodium hydrogen carbonate) only.

To calculate the number of moles for given molarity, we use the equation:

`\text{Molarity of the solution}=\frac{\text{Moles of solute}* 1000}{\text{Volume of solution (in mL)}}`

• For hydrochloric acid:

Molarity of hydrochloric acid = 0.15 M

Volume of solution = 3 mL

Putting values in above equation, we get:

`0.15M=\frac{\text{Moles of hydrochloric acid}* 1000}{3mL}\\\\\text{Moles of hydrochloric acid}=0.00045mol`

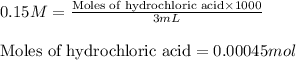
• For sodium hydrogen carbonate:

Molarity of sodium hydrogen carbonate = 0.025 M

Volume of solution = 150 mL

Putting values in above equation, we get:

`0.025M=\frac{\text{Moles of sodium hydrogen carbonate}* 1000}{150mL}\\\\\text{Moles of sodium hydrogen carbonate}=0.00375mol`

• For carbonic acid:

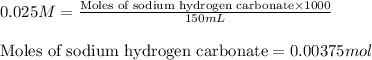
Molarity of carbonic acid = 0.045 M

Volume of solution = 150 mL

Putting values in above equation, we get:

`0.045M=\frac{\text{Moles of carbonic acid}* 1000}{150mL}\\\\\text{Moles of carbonic acid}=0.00675mol`

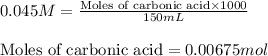
The chemical reaction for sodium hydrogen carbonate and hydrochloric acid follows the equation:

`NaHCO_3+HCl\rightarrow NaCl+H_2CO_3`

Initial: 0.00375 0.00045 0.00675

Final: 0.00330 - 0.00720

Volume of solution = 150 + 3 = 153 mL = 0.153 L (Conversion factor: 1 L = 1000 mL)

To calculate the pH of acidic buffer, we use the equation given by Henderson Hasselbalch:

`pH=pK_a+\log(([salt])/([acid]))`

`pH=pK_a+\log(([NaHCO_3])/([H_2CO_3]))`

We are given:

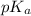`pK_a` = negative logarithm of acid dissociation constant of carbonic acid = 6.37

`[NaHCO_3]=(0.0033)/(0.153)`

`[H_2CO_3]=(0.0072)/(0.153)`

pH = ?

Putting values in above equation, we get:

`pH=6.37+\log((0.0033/0.153)/(0.0072/0.153))\\\\pH=6.03`

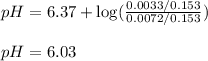
Hence, the new pH of the solution is 6.03