Answer:
v = 1.15*10^{7} m/s
Step-by-step explanation:
given data:
charge/ unit area
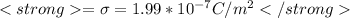
plate seperation = 1.69*10^{-2} m
we know that
electric field btwn the plates is
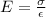
force acting on charge is F = q E
Work done by charge q id
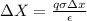
this work done is converted into kinectic enerrgy
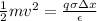
solving for v
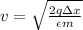
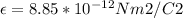

v = 1.15*10^{7} m/s