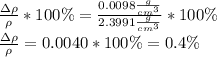Answer:
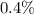
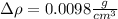
Step-by-step explanation:
Recall that density is defined as
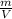 and that relative uncertainty is defined as
and that relative uncertainty is defined as
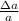 where
where
 is the uncertainty in the measure and a the measure, To find the uncertainty when two physical quantities are divided, their relative uncertainties are added and then multiplied with the division result of the quantities.
is the uncertainty in the measure and a the measure, To find the uncertainty when two physical quantities are divided, their relative uncertainties are added and then multiplied with the division result of the quantities.
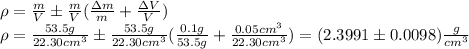
We have:
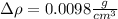
To find the percent uncertainty, we multiply the relative uncertainty by 100%.