Question

A box moving on a horizontal surface with an initial velocity of 20 m/s slows to a stop over a time period of 5.0 seconds due solely to the effects of friction. What is the coefficient of kinetic friction between the box and the ground?

Answer 1

μ= 0.408 : coefficient of kinetic friction

Step-by-step explanation:

Kinematic equation for the box:

`a=(v_(f) -v_(i) )/(t)` Formula( 1)

a= acceleration

v_i= initial speed =0

v_f= final speed= 20 m/s

t= time= 5 s

We replace data in the formula (1):

`a=(0-20)/(5)`

`a= -(20)/(5)`

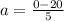
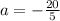
a= - 4m/s²

Box kinetics: We apply Newton's laws in x-y:

∑Fx=ma : second law of Newton

-Ff= ma Equation (1)

Ff is the friction force

Ff=μ*N Equation (2)

μ is the coefficient of kinetic friction

N is the normal force

Normal force calculation

∑Fy=0 : Newton's first law

N-W=0 W is the weight of the box

N=W= m*g : m is the mass of the box and g is the acceleration due to gravity

N=9.8*m

We replace N=9.8m in the equation (2)

Ff=μ*9.8*m

Coefficient of kinetic friction ( μ) calculation

We replace Ff=μ*9.8*m and a= -4m/s² in the equation (1):

-μ*9.8*m: -m*4 : We divide by -m on both sides of the equation

9.8*μ=4

μ=4 ÷ 9.8

μ= 0.408