Assume that 155 students are surveyed and every student takes at least one of the following languages. The results of the survey are as follows: 90 take French. 83 take German. 42 take French and German. - QAmmunity.org

Assume that 155 students are surveyed and every student takes at least one of the following languages. The results of the survey are as follows: 90 take French. 83 take German. 42 take French and German.

asked Jun 7, 2020 42.7k views

1 Answer

Answer:

91 people take Russian

26 people take French and Russian but not German

Explanation:

To solve this problem, we must build the Venn's Diagram of this set.

I am going to say that:

-The set A represents the students that take French.

-The set B represents the students that take German

-The set C represents the students that take Russian.

We have that:

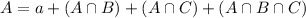
$A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)$

In which a is the number of students that take only Franch, A \cap B is the number of students that take both French and German , A \cap C is the number of students that take both French and Russian and A \cap B \cap C is the number of students that take French, German and Russian.

By the same logic, we have:

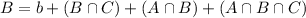
$B = b + (B \cap C) + (A \cap B) + (A \cap B \cap C)$

$C = c + (A \cap C) + (B \cap C) + (A \cap B \cap C)$

This diagram has the following subsets:

$a,b,c,(A \cap B), (A \cap C), (B \cap C), (A \cap B \cap C)$

There are 155 people in my school. This means that:

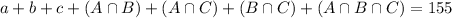
$a + b + c + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 155$

The problem states that:

90 take Franch, so:

A = 90

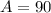
83 take German, so:

B = 83

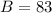
22 take French, Russian, and German, so:

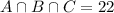
$A \cap B \cap C = 22$

42 take French and German, so:

$A \cap B = 42 - (A \cap B \cap C) = 42 - 22 = 20$

41 take German and Russian, so:

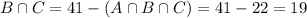
$B \cap C = 41 - (A \cap B \cap C) = 41 - 22 = 19$

22 take French as their only foreign language, so:

a = 22

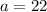
Solution:

(1) How many take Russian?

$C = c + (A \cap C) + (B \cap C) + (A \cap B \cap C)$

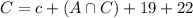
$C = c + (A \cap C) + 19 + 22$

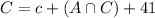
$C = c + (A \cap C) + 41$

First we need to find
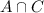$A \cap C$ , that is the number of students that take French and Russian but not German. For this, we have to go to the following equation:

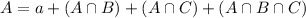
$A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)$

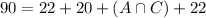
$90 = 22 + 20 + (A \cap C) + 22$

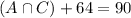$(A \cap C) + 64 = 90$ .

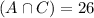
$(A \cap C) = 26$

----------------------------

The number of students that take Russian is:

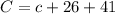
C = c + 26 + 41

C = c + 67

------------------------------

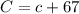
Now we have to find c, that we can find in the equation that sums all the subsets:

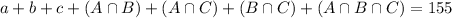
$a + b + c + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 155$

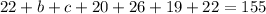
22 + b + c + 20 + 26 + 19 + 22 = 155

b + c + 109= 155

b + c = 46

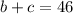
For this, we have to find b, that is the number of students that take only German. Then we go to this eqaution:

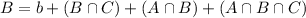
$B = b + (B \cap C) + (A \cap B) + (A \cap B \cap C)$

B = b + 19 + 20 + 22

B = b + 61

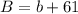
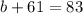
b + 61 = 83

b = 22

-------

b + c = 46

c = 46 - b

c = 24

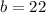
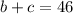
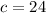
The number of people that take Russian is:

C = c + 67

C = 24 + 67

C = 91

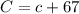
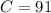
91 people take Russian

(2) How many take French and Russian but not German?

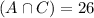
$(A \cap C) = 26$

26 people take French and Russian but not German

AnMaree answered Jun 11, 2020

5.2k points

Search QAmmunity.org