Question

A hot-air balloon is descending at a rate of 2.1 m/s when a passenger drops a camera. If the camera is 42 m above the ground when it is dropped, how long does it take for the camera to reach the ground?

Express your answer using two significant figures.
If the camera is 42 m above the ground when it is dropped, what is its velocity just before it lands? Let upward be the positive direction for this problem.
Express your answer using two significant figures.

Answer 1

a) 2.7s

b) 29 m/s

Step-by-step explanation:

The equation for the velocity and position of a free fall are the following

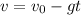`v=v_(0)-gt` -(1)

`x=x_(0)+v_(0)t-gt^(2)/2` - (2)

Since the hot-air ballon is descending at 2.1m/s and the camera is dropped at 42 m above the ground:

`v_(0)=-2.1m/s`

`x_(0)=42m`

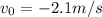
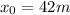
To calculate the time which it takes to reach the ground we use eq(2) with x=0, and look for the positive solution of t:

`t = (1)/(84)(2.1\pm\sqrt{2.1^(2) - 4*42*9.81/2} )`

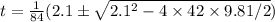
t = 2.71996

Rounding to two significant figures:

t = 2.7 s

Now we calculate the velocity the camera had just before it lands using eq(1) with t=2.7s

`v=-2.1-9.81*(2.71996)`

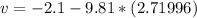
v = -28.782 m/s

Rounding to two significant figures:

v = -29 m/s

where the minus sign indicates the downwards direction