Question

Given a particle that follows the acceleration a(t) 10 (-t + 2 ) (t-5)+ 100 m/s2, find: a. Find the displacement at 2 seconds. Assume from rest and a starting point of 3m. b. Find the velocity at 4 seconds. Assume an initially at rest. c. Find the time at which maximum displacement occurs (use calculus because it is way easier, not kinematics). d. Find the value of maximum velocity over the interval 0

Answer 1

a. x= 83.03 m at t= 2 s

b. v=346.7 m/s at t= 4s

c. t=10.5s : maximum displacement occurs

d. t= 7s : maximum velocity

Step-by-step explanation:

Definitions

acceleration :a(t) = dv/dt :Derived from velocity with respect to time

Velocity : V(t)=dx/dt : Derived from Displacement: with respect to time

Displacement: X(t)

Developing of problem

we have a(t) =10 (-t + 2 ) (t-5)+ 100

a(t) =(-10 t + 20) (t-5)+ 100 = -10 t²+50t+ 20t-100+ 100=--10 t²+70t

a(t)=--10 t²+70t Equation (1)

a(t) = dv/dt

-10 t²+70t=dv/dt

dv=(-10 t²+70t)dt

We apply integrals to both sides of the equation

∫dv=∫(-10 t²+70t)dt

`v=(-10t^(3) )/(3)   +(70t^(2) )/(2) +C_(1)`

`v=(-10t)/(3) +35t^(2) +C_(1)`

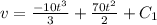
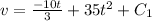
at time t=0, v=0, then, C₁=0

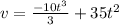`v=(-10t^(3))/(3) +35t^(2)}` Equation (2)

`v=(dx)/(dt)`

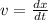
dx= vdt

We apply integrals to both sides of the equation and we replace v(t) of the equation (2)

`\int\limits {\, dx =\int\limits{((-10t^(3) )/(3)+35t^(2) ) } \, dt`

`x=(-5t^(4) )/(6) +(35t^(3) )/(3) +C_(2)`

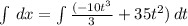
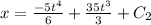
at time t=0, x=3, then,C₂=3

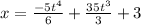`x=(-5t^(4) )/(6) +(35t^(3) )/(3) +3}` Equation (3)

a)Displacement at t=2s

We replace t=2s in the Equation (3)

`x=(-5(2)^(4) )/(6) +(35(2)^(3) )/(3) +3}`

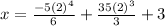
x= 83.03 m at t= 2 s

b) Velocity at t=4s

We replace t=4s in the Equation (2)

`v=(-10(4)^(3))/(3) +35(4)^(2)}`

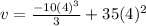
v=346.7 m/s at t= 4s

c)Time at which maximum displacement occurs

at maximum displacement :v=
`(dx)/(dt) =0`

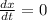
in the Equation (2) :

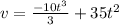`v=(-10t^(3))/(3) +35t^(2)}` =0

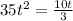`35t^(2) } =(10t)/(3)` ,we divide by t on both sides of the equation

`t=(35*3)/(10)`

t=10.5s

d. maximum velocity over the interval

at maximum velocity :a=
`(dv)/(dt) =0`

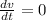
in the Equation (1)

-10 t²+70t = 0 we multiply the equation by -1 and factor

10t ( t-7) =0

t= 7 s