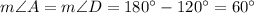Question

Given: ABCD trapezoid, BK ⊥ AD , AB=DC AB=8, AK=4 Find: m∠A, m∠B

Answer 1

`m\angle B=m\angle C=120^(\circ)`

`m\angle A=m\angle D=60^(\circ)`

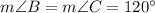
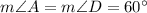
Explanation:

Trapezoid ABCD is isosceles trapezoid, because AB = CD (given). In isosceles trapezoid, angles adjacent to the bases are congruent, then

• 
  `\angle A\cong \angle D;`
• 
  `\angle B\cong \angle C.`

Since BK ⊥ AD, the triangle ABK is right triangle. In this triangle, AB = 8, AK = 4. Note that the hypotenuse AB is twice the leg AK:

`AB=2AK.`

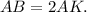
If in the right triangle the hypotenuse is twice the leg, then the angle opposite to this leg is 30°, so,

`m\angle ABK=30^(\circ)`

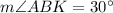
Since BK ⊥ AD, then BK ⊥ BC and

`m\angle KBC=90^(\circ)`

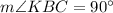
Thus,

`m\angle B=30^(\circ)+90^(\circ)=120^(\circ)\\ \\m\angle B=m\angle C=120^(\circ)`

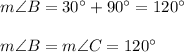
Now,

`m\angle A=m\angle D=180^(\circ)-120^(\circ)=60^(\circ)`