Question

Determine which of the following sets of three points constitute the vertices of a right triangle: (a) 3 + 5i,2 +2i,5i; (b)2i,3 + 5i,4 + i; (c)6 +4i,7 + 5i, 8 +4i

Answer 1

Option (c) is correct

Explanation:

Case (a)

A = 3 + 5i = (3, 5)

B = 2 + 2i = (2, 2)

C = 5i = (0, 5)

Use the distance formula to find the distance between two points

`AB = \sqrt{(2-3)^(2)+(2-5)^(2)}=√(10)`

`BC = \sqrt{(0-2)^(2)+(5-2)^(2)}=√(13)`

`CA = \sqrt{(0-3)^(2)+(5-5)^(2)}=√(9)`

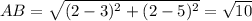
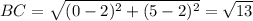
For the triangle to be right angles triangle

`BC^(2)=AB^(2)+CA^(2)`

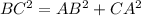
Here, it is not valid, so these are not the points of a right angled triangle.

Case (b)

A = 2i = (0, 2)

B = 3 + 5i = (3, 5)

C = 4 + i = (4, 1)

Use the distance formula to find the distance between two points

`AB = \sqrt{(3-0)^(2)+(5-2)^(2)}=√(18)`

`BC = \sqrt{(4-3)^(2)+(1-5)^(2)}=√(17)`

`CA = \sqrt{(4-0)^(2)+(1-2)^(2)}=√(17)`

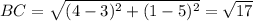
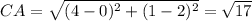
For the triangle to be right angles triangle

`AB^(2)=BC^(2)+CA^(2)`

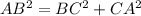
Here, it is not valid, so these are not the points of a right angled triangle.

Case (c)

A = 6 + 4i = (6, 4)

B = 7 + 5i = (7, 5)

C = 8 + 4i = (8, 4)

Use the distance formula to find the distance between two points

`AB = \sqrt{(7-6)^(2)+(5-4)^(2)}=√(2)`

`BC = \sqrt{(8-7)^(2)+(4-5)^(2)}=√(2)`

`CA = \sqrt{(8-6)^(2)+(4-4)^(2)}=√(4)`

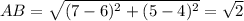
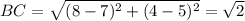
For the triangle to be right angles triangle

`CA^(2)=BC^(2)+AB^(2)`

Here, it is valid, so these are the points of a right angled triangle.