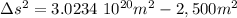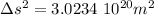Answer:
- a.
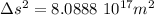
- b.
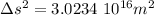
- c.
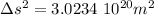
Step-by-step explanation:
The spacetime interval
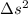 is given by
is given by
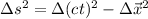
please, be aware this is the definition for the signature ( + - - - ), for the signature (- + + + ) the spacetime interval is given by:
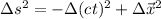 .
.
Lets work with the signature ( + - - - ), and, if needed in the other signature, we can multiply our interval by -1.
a.
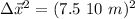
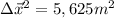
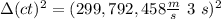
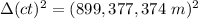
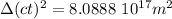
so
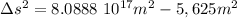
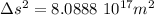
b.
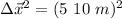
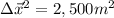
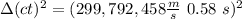
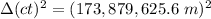
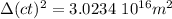
so

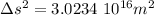
c.
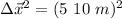
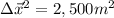
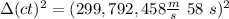
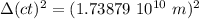
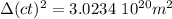
so