Question

Use the given data at 500 K to calculate ΔG°for the reaction

2H2S(g) + 3O2(g) → 2H2O(g) + 2SO2(g)

Substance H2S(g) O2(g) H2O(g) SO2(g)
ΔH°f(kJ/mol) -21 0 -242 -296.8
S°(J/K·mol) 206 205 189 248

Answer 1

Answer : The value of
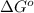`\Delta G^o` for the reaction is -959.1 kJ

Explanation :

The given balanced chemical reaction is,

`2H_2S(g)+3O_2(g)\rightarrow 2H_2O(g)+2SO_2(g)`

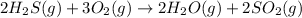
First we have to calculate the enthalpy of reaction
`(\Delta H^o)`.

`\Delta H^o=H_f_(product)-H_f_(reactant)`

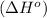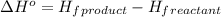
`\Delta H^o=[n_(H_2O)* \Delta H_f^0_((H_2O))+n_(SO_2)* \Delta H_f^0_((SO_2))]-[n_(H_2S)* \Delta H_f^0_((H_2S))+n_(O_2)* \Delta H_f^0_((O_2))]`

where,

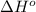`\Delta H^o` = enthalpy of reaction = ?

n = number of moles

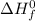`\Delta H_f^0` = standard enthalpy of formation

Now put all the given values in this expression, we get:

`\Delta H^o=[2mole* (-242kJ/mol)+2mole* (-296.8kJ/mol)}]-[2mole* (-21kJ/mol)+3mole* (0kJ/mol)]`

`\Delta H^o=-1035.6kJ=-1035600J`

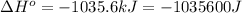
conversion used : (1 kJ = 1000 J)

Now we have to calculate the entropy of reaction
`(\Delta S^o)`.

`\Delta S^o=S_f_(product)-S_f_(reactant)`

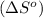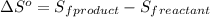
`\Delta S^o=[n_(H_2O)* \Delta S_f^0_((H_2O))+n_(SO_2)* \Delta S_f^0_((SO_2))]-[n_(H_2S)* \Delta S_f^0_((H_2S))+n_(O_2)* \Delta S_f^0_((O_2))]`

where,

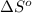`\Delta S^o` = entropy of reaction = ?

n = number of moles

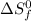`\Delta S_f^0` = standard entropy of formation

Now put all the given values in this expression, we get:

`\Delta S^o=[2mole* (189J/K.mol)+2mole* (248J/K.mol)}]-[2mole* (206J/K.mol)+3mole* (205J/K.mol)]`

`\Delta S^o=-153J/K`

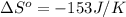
Now we have to calculate the Gibbs free energy of reaction
`(\Delta G^o)`.

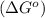As we know that,

`\Delta G^o=\Delta H^o-T\Delta S^o`

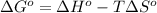
At room temperature, the temperature is 500 K.

`\Delta G^o=(-1035600J)-(500K* -153J/K)`

`\Delta G^o=-959100J=-959.1kJ`

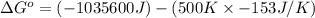
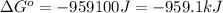
Therefore, the value of
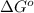`\Delta G^o` for the reaction is -959.1 kJ