Question

Consider the differential equation y'+\lambda y=e^{-t}, when \lambda is some constant.

(a) Find all values of \lambda such that all solutions tend to zero as t \rightarrow infinity .

(b) At least one solution goes to zero as t \rightarrow infinity .

Answer 1

Part a) value of
`\lambda` such that all the solutions tend to zero equals 1.

Part b)

For a particular solution to tend to 0 will depend on the boundary conditions.

Explanation:

The given differential equation is

`y'+\lambda y=e^(-t)`

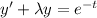
This is a linear differential equation of first order of form
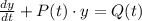`(dy)/(dt)+P(t)\cdot y=Q(t)` whose solution is given by

`y\cdot e^(\int P(t)dt)=\int e^(\int P(t)dt)\cdot Q(t)dt`

Applying values we get

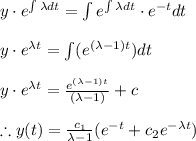
`y\cdot e^(\int \lambda dt)=\int e^(\int \lambda dt)\cdot e^(-t)dt\\\\y\cdot e^(\lambda t)=\int (e^((\lambda -1)t))dt\\\\y\cdot e^(\lambda t)=(e^((\lambda -1)t))/((\lambda -1))+c\\\\\therefore y(t)=(c_(1))/(\lambda -1)(e^(-t)+c_(2)e^(-\lambda t))`

here
`c_(1),c_(2)` are arbitrary constants

part 1)

For all the function to approach 0 as t approaches infinity we have

`y(t)=\lim_(t\to \infty )[(c_(1))/(\lambda -1)(e^(-t)+c_(2)e^(-\lambda t))]\\\\y(\infty )=(c_(1))/(\lambda -1)=0\\\\\therefore \lambda =1`

Part b)

For a particular solution to tend to 0 will depend on the boundary conditions as
`c_(1),c_(2)` are arbitrary constants