Answer:
a) 200m, 100m/s
b) 710.20m
c) -117.98 m/s
d) 26.24 s
Step-by-step explanation:
To solve this we have to use the formulas corresponding to a uniformly accelerated motion problem:
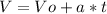 (1)
(1)
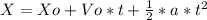 (2)
(2)
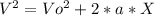 (3)
(3)
where:
Vo is initial velocity
Xo=intial position
V=final velocity
X=displacement
a)
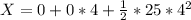
the intial position is zero because is lauched from the ground and the intial velocitiy is zero because it started from rest.
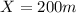
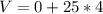

b)
The intial velocity is 100m/s we know that because question (a) the acceleration is -9.8
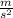 because it is going downward.
because it is going downward.
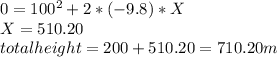
c)
In order to find the velocity when it crashes, we can use the formula (3).
the initial velocity is 0 because in that moment is starting to fall.
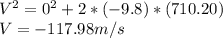
the minus sign means that the object is going down.
d)
We can find the total amount of time adding the first 4 second and the time it takes to going down.
to calculate the time we can use the formula (2) setting the reference at 200m:
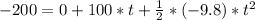
solving this we have: time taken= 22.24 seconds
total time is:
total=22.24+4=26.24 seconds.