Answer with explanation:
The number of letters in word "ALGORITHM" = 9
The number of combinations to select r things from n things is given by :-
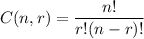
Now, the number of combinations to select 6 letters from 9 letters will be :-
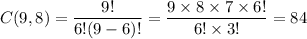
Thus , the number of ways can six of the letters of the word ALGORITHM=84
The number of ways to arrange n things in a row :
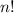
So, the number of ways can the letters of the word ALGORITHM be arranged in a be seated together in the row :-
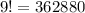
If GOR comes together, then we consider it as one letter, then the total number of letters will be = 1+6=7
Number of ways to arrange 9 letters if "GOR" comes together :-
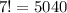
Thus, the number of ways to arrange 9 letters if "GOR" comes together=5040