Question

How many ways can six of the letters of the word ALGORITHM be selected 8. How many ways can the letters of the word ALGORITHM be arranged in a be seated together in the row? and written in a row? row if the letters GOR must remain together (in this order)?

Answer 1

Answer with explanation:

The number of letters in word "ALGORITHM" = 9

The number of combinations to select r things from n things is given by :-

`C(n,r)=(n!)/(r!(n-r)!)`

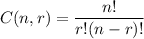
Now, the number of combinations to select 6 letters from 9 letters will be :-

`C(9,8)=(9!)/(6!(9-6)!)=(9*8*7*6!)/(6!*3!)=84`

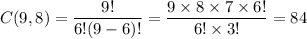
Thus , the number of ways can six of the letters of the word ALGORITHM=84

The number of ways to arrange n things in a row :
`n!`

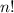
So, the number of ways can the letters of the word ALGORITHM be arranged in a be seated together in the row :-

`9!=362880`

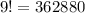
If GOR comes together, then we consider it as one letter, then the total number of letters will be = 1+6=7

Number of ways to arrange 9 letters if "GOR" comes together :-

`7!=5040`

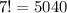
Thus, the number of ways to arrange 9 letters if "GOR" comes together=5040