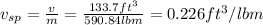Question

A 133.7 ft3 volume of liquid hydrogen rocket fuel has a mass of 268 kg. Calculate: the weight of the fuel at standard (Earth) sea level conditions in N and Ibr, the density of the fuel in kg/m3, and the specific volume in ft3/lbm (Ibm=pound-mass, which is not the same as a a lbf or a slug)

Answer 1

First, let's make some convertions:

`268kg*(1 lbm)/(0.454kg)= 590.84 lbm`

`133.7 ft^3*(1m^3)/(35.3147ft^3) = 3.78m^3`

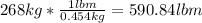
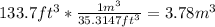
a) weight of the fuel:

Newtons: The weight in newtons is equal to the mass in kilograms times the gravity in m/s^2.

`W = m*g = 268kg*9.81m/s^2=2629.08 N`

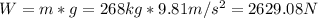
lbf: The weight inlbf is equal to the mass in slugs times the gravity in ft/s^2.

`W= m*g = 590.84 lbm *(1 slug)/(32.174lbm) *32.174ft/s^2 = 590.84 lbf`

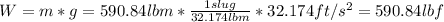
b) density:

The density is the mass in kg of the fuel divided by its volume in m^3:

`d = (m)/(v) =(268kg)/(3.78m^3) =70.9 kg/m^3`

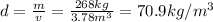
c) specific volume:

The specific volume is the volume in ft^3 of the fuel divided by its mass in lbm:

`v_(sp) = (v)/(m) =(133.7 ft^3)/(590.84 lbm) = 0.226 ft^3/lbm`