Question

An elevator moves downward in a tall building at a constant speed of 5.70 m/s. Exactly 4.95 s after the top of the elevator car passes a bolt loosely attached to the wall of the elevator shaft, the bolt falls from rest. (a) At what time does the bolt hit the top of the still-descending elevator? (Assume the bolt is dropped at t = 0 s.)(b) Estimate the highest floor from which the bolt can fall if the elevator reaches the ground floor before the bolt hits the top of the elevator. (Assume 1 floor congruent 3 m.)

Answer 1

a) t = 3.01s

b) 15th floor

Step-by-step explanation:

First we need to know the distance the elevator has descended before the bolt fell.

`\Delta Y_(e) = -V_(e)*t = -5.7 * 4.95 = -28.215m`

Now we can calculate the time that passed before both elevator and bolt had the same position:

`Y_(b)=Y_(e)`

`Y_(ob)+V_(ob)*t-g*(t^(2))/(2) = Y_(oe) - V_(e)*t`

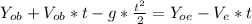
`0+0-5*t^(2) = -28.215 - 5.7*t` Solving for t:

t1 = -1.87s t2 = 3.01s

In order to know how the amount of floors, we need the distance the bolt has fallen:

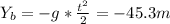`Y_(b)=-g*(t^(2))/(2)=-45.3m` Since every floor is 3m:

Floors = Yb / 3 = 15 floors.