Question

Water leaks from a vertical cylindrical tank through a small hole in its base at a volumetric rate proportional to the square root of the volume of water remaining. The tank initially contains 300 liters and 22 liters leak out during the first day A. When will the tank be half empty?t16 day (include units.) B. How much water will remain in the tank after 5 days? volume 198 L (include units)

Answer 1

After 7.84 the tank be half empty. The water remain in the tank after 5 days is 198.401 L.

Explanation:

Consider the provided information.

It is given that a small hole in its base at a rate proportional to the square root of the volume of water remaining. The tank initially contains 300 liters and 22 liters leak out during the first day.

The rate of water leak can be written as:

`(dV)/(dt)\propto √(V)`

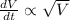
Let k be the constant of proportionality.

`(dV)/(dt)=k √(V)`

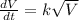
Integrate both the sides as shown:

`(dV)/(√(V))=k dt\\\int(dV)/(√(V))=\int k dt\\2√(V) =kt+c`

Since for t=0 the volume was 300.

`2√(300) =k(0)+c\\20√(3) =c\\c=34.641`

Now substitute the value of c in above equation.

`2√(V) =kt+34.641`

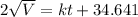
22 liters leak out during the first day, thus now the remaining volume is 300-22=278 liters.

`2√(278) =k(1)+34.641\\33.347 =k+34.641\\k=33.347 -34.641\\k=-1.294`

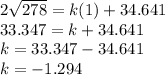
Thus, the required equation is:
`2√(V) =-1.294t+34.641`

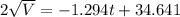
Part (A) When will the tank be half empty.

Substitute v=150 liters for half empty in above equation.

`2√(150) =-1.294t+34.641`

`24.495 =-1.294t+34.641`

`-10.146 =-1.294t`

`t=7.84`

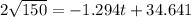
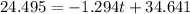
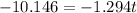
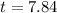
Hence, after 7.84 the tank be half empty.

Part (B) How much water will remain in the tank after 5 days.

Substitute the value of t=5 in
`2√(V) =-1.294t+34.641`

`2√(V) =-1.294(5)+34.641`

`2√(V) =28.171`

`√(V) =14.0855`

`V =198.401`

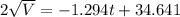
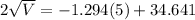
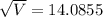
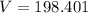
Hence, the water remain in the tank after 5 days is 198.401 L.