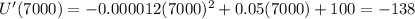Answer:
a.
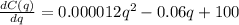
b.
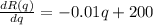
c.
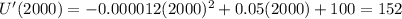
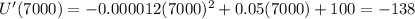
Explanation:
a) The marginal cost function is given by the derivative of the total cost function, in this way the marginal cost function for this company is:
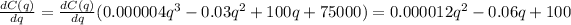
b) The income function is given by the relation
 .
.
The marginal revenue function for the company is given by the derivative of the revenue function, in this way the marginal revenue function is:
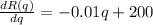
(c) The profit function of the company is given by the relation
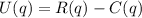 , and the marginal utility function is given by the derivative of the utility function, in this way , the marginal utility function is:
, and the marginal utility function is given by the derivative of the utility function, in this way , the marginal utility function is:

When q = 2000, the marginal utility is:
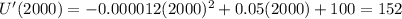
When q = 7000, the marginal utility is: