Question

A ball is thrown with velocity of 10 m/s upwards. If the ball is caught 1 m above its initial position, what is the speed of the ball when it is caught?

Answer 1

v = 8.96 m/s

Step-by-step explanation:

Initial speed of the ball, u = 10 m/s

It caught 1 meter above its initial position.

Acceleration due to gravity,
`g=-9.8\ m/s^2`

We need to find the final speed of the ball when it is caught. Let is equal to v. To find the value of v, use third equation of motion as :

`v^2-u^2=2as`

`v^2=2as+u^2`

`v^2=2(-9.8)* 1+(10)^2`

v = 8.96 m/s

So, the speed of the ball when it is caught is 8.96 m/s. Hence, this is the required solution.

Answer 2

8.96 m/s, upward direction

Step-by-step explanation:

Given that, the initial velocity of the ball is,

`u=10m/s`

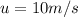
And the acceleration in the downward direction is positive but in this situation the acceleration will be negative so,

`a=9.8(m)/(s^(2) )`

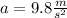
And according to question vertical displacement is,

`s=1m`

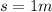
Now suppose v be the final velocity of the ball.

Applying third equation of motion,

`v^(2)=u^(2)+2as`

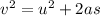
Here, u is the initial velocity, a is the acceleration, s is the displacement.

Substitute all the variables.

`v=\sqrt{10^(2)+2(-9.8)* 1 } \\v=√(80.4)\\ v=8.96(m)/(s)`

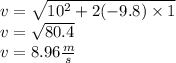
Therefore, the speed of ball when it is caught is 8.96 m/s in the upward direction.