Question

Suppose that we choose inches as our basic unit of distance and days as our basic unit of time. a. What would the units of velocity and acceleration be in this system? Explain. b. Would this be a good choice of units for measuring the acceleration of an automobile? Explain.

Answer 1

a)

velocity unit =
`(inches)/(days)`

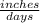
acceleration unit =
`(inches)/(days^(2) )`

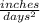
b) No

Step-by-step explanation:

a)

Velocity is a vector expression of the displacement respect to time of something, with magnitude and a defined direction. Then, to know the magnitude of the vector (v) we have to divide the distance (Δx) by the time (Δt) it takes to travel that distance:

v = Δx / Δt

Besides, the unit of velocity is a compound unit between distance units and time units. If we choose inches as our basic unit of distance and days as our basic unit of time, then the unit of velocity would be:

`(inches)/(days)`

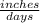
On the other hand, acceleration is a vector defined as the rate at which an object changes its velocity. The math expression divides the change o velocity (Δv) by the time (Δt) it takes to make this change to obtain the acceleration magnitude (a):

a = Δv / Δt

So, the unit of acceleration is a compound unit between velocity units and time units. Again, if we choose inches as our basic unit of distance and days as our basic unit of time, then the unit of velocity in this system would be
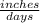`(inches)/(days)` , as shown. Finally, the unit of acceleration would be:

`(inches)/(days^(2) )`

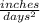
In resume:

velocity unit =
`(inches)/(days)`

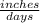
acceleration unit =
`(inches)/(days^(2) )`

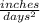
b)

To answer whether this units´ system is a good choice or not for measuring the acceleration of an automobile, let´s think about its normal values.

A car normally takes between 4 to 8 seconds to change its velocity from 0 to 100 km/h, then normal acceleration values for the media of 6 seconds (or its equivalent in hours 0.0016 h) are:

a = Δv / Δt =
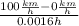`(100(km)/(h)-0(km)/(h) )/(0.0016 h)` = 62,500
`(km)/(h^(2) )`

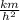
If we want to use the units system of this exercise, then we have to use the equivalences between inches and kilometers (1 km = 39,370.1 inches) and the other between days and hours (24 h = 1 day). Then,

a = 62,500
`(km)/(h^(2) )` *
`(39370.1 inches)/(1 km)` *
`((24 h)/(1 days)) ^(2)`

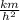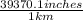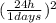
a = 62500
`(km)/(h^(2) )` *
`(39,370.1 inches)/(1 km)` *
`(576 h^(2) )/(days^(2) )`

a = 1.42 ˣ10¹²
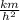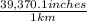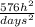
`(inches)/(days^(2) )`

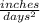
If we choose this units´ system to express the acceleration of an automobile, it results in a very high number that introduces a difficulty just to quantify the acceleration. Then, this system is not a good choice for that purpose.