Question

10,101 base 2 + 11,011 base 2 =

Answer 1

110,000 base 2

Explanation:

column 1 [the first position in the number]:

1+1=0, (carry 1)

column 2:

0+1 +1 (carried)=0, (carry 1)

column 3:

1+0+1 (carried)=0, (carry 1)

column 4:

0+1+1 (carried)=0, (carry 1)

column 5:

1+1+1=1, (carry 1)

then you write the last 1 'cause there is n number to add with:

`10,101_(2)+11,011_(2)=110,000_(2)`

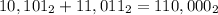
In binary system the highest number to write is 1, if you add 1+1, it jumps to 0, and you have to carry 1 to the next position.

If you are not sure about the sum, you can convert the numbers in base 2, to base 10, so you can know if it is correct:

`10,101_(2)=21_(10)\\11,011_(2)=27_(10)\\110,000_(2)=48_(10)`

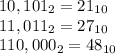
So 21+27=48.

In decimal system when you add 9+1, it jumps to 0 and then you have to carry 1 to the next position, because the the highest number you can write is 9.