Question

A charge 5.00 nC is placed at the origin of an xy-coordinate system, and a charge -1.97 nC is placed on the positive x-axis at x = 4.00 cm . A third particle, of charge 6.05 nC is now placed at the point x = 4.00 cm , y= 3.02 cm . Q: Find the y-component of the total force exerted on the third charge by the other two

Answer 1

The total force exerted on the Y axis is: -52.07μC

Step-by-step explanation:

This is an electrostatic problem, so we will use the formulas from the Coulomb's law:

`F=k*(Q*Q')/(r^2)\\where:\\k=coulomb constant\\r=distance\\Q=charge`

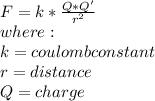
We are interested only of the effect of the force on the Y axis. We can notice that the charge placed on the x=4cm will exers a force only on the Y axis so:

`Fy1=9*10^9*(6.05*10^(-9)*(-1.97)*10^(-9))/((3.02*10^(-2))^2)\\`

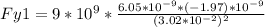
Fy1=-117.61μC

For the charge placed on the origin we have to calculate the distance and the angle:

`r=\sqrt{(4*10^(-2)m)^2 +(3.02*10^(-2)m)^2} \\r=5cm=0.05m`

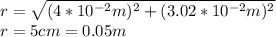
we can find the angle with:

`alpha = arctg((3.02cm)/(4cm))=37^o`

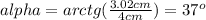
The for the Force on Y axis is:

`Fy2=9*10^9*(6.05*10^(-9)*(5)*10^(-9))/((3.02*10^(-2))^2)*sin(37^o)\\`

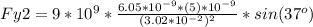
Fy2=65.54μC

The total force exerted on the Y axis is:

Fy=Fy1+Fy2=-52.07μC