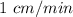Answer:
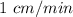
Explanation:
Let V be the volume of cube and x be it's side .
We know that volume of cube is
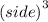 i.e.,
i.e.,
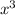
Given :
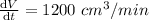
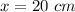
To find :
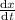
Solution :
Consider equation
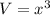
On differentiating both sides with respect to t , we get
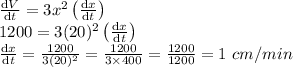
So,
Length of the side is increasing at the rate of