Answer:
A proof can be as follows:
Explanation:
Remember that an odd interger is of the form
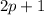 where
where
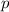 is a integer and remember that two consecutive integer are two numbers of the form
is a integer and remember that two consecutive integer are two numbers of the form
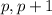
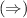 Suppose the
Suppose the
 is an odd integer.
is an odd integer.
Then
 must be an even integer and hence divisible by 2. Then we define
must be an even integer and hence divisible by 2. Then we define
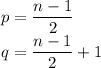
Then we have that
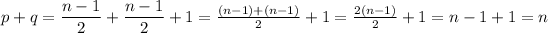
The converse is as follows:
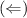 Let
Let
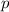 an integer, then
an integer, then
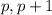 are two consecutive integers. Then
are two consecutive integers. Then
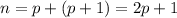 is an odd integer.
is an odd integer.