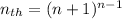Question

Exercise 4.x2 Make a reasonable conjecture about the nth term in the sequence. 1 3 16 125 1296...

Answer 1

The nth term in the sequence is given by the equation:

`n_(th) =(n+1)^(n-1)`

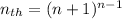
Explanation:

Arranging a table for n and nth:

`\left[\begin{array}{ccc}n&nth\\1&1\\2&3\\2&16\\4&125\\5&1296\end{array}\right]`

It is easier to notice that 16 and 125 result from the second power of 4 and the third of 5, respectively, which are one number below their respective position. That is why we can deduce that the base of the power is n+1.

For n=2, the base n+1 results in 3, which matches the nth term for n=2. Since 3 is the result of 3 to the power of 1, 16 is 4 to the power of 2, and 125 is 5 to the power of 3, all the powers are one number behind n, so the power is given by n-1, giving the equation:

`n_(th) =(n+1)^(n-1)`