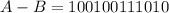Question

Let A be the set represented by the bitstring 01011011100, let B be the set represented by the bitstring 10110111010. Find the bitstrings representing Ac, AUB, AnB, and A-E.

Answer 1

Ac = 10100100011

`A \cup B = 11111111110`

`A \cap B = 00010011000`

`A - B = 100100111010`

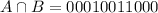
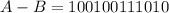
Explanation:

All these operations are bitwise operations.

Ac is the complement of a. So where we have a bit 0, the complement is 1. Where we have a bit 1, the complement is 0. So

A = 01011011100

Ac = 10100100011

The second operation is the union between A and B. This is bitwise(bit 1 of A with bit 1 of B, bit 2 of A with bit 2 of B,...). The union operation is only 0 when it is between two zeros. So:

A = 01011011100

B = 10110111010

`A \cup B = 11111111110`

The third operation is the intersection between A and B. Again, bitwise. The intersection is only 1 when it is between two bits that are 1. So

A = 01011110100

B = 10110111010

`A \cap B = 00010011000`

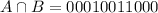
The last operation is the bitwise subtraction between A and B. We start from the least significant bit(the last one). And we have to take care of the borrow operator also, similarly to a decimal subtraction.

We can only borrow from a previous bit 1, and this bit is set to 0

0-0 is 0 with no borrow

1-0 is 1 with no borrow

1 with borrow - 0 is 1 with borrow

1 with borrow - 1 is 1 with no borrow

0-1 is 1 with no borrow

0 with borrow -1 is 0 with no borrow

1-1 is 0 with no borrow

If we arrive at the first bit(the most significant) with a borrow, we must add a 1 at the front of the answer. So

A = 01011110100

B = 10110111010

`A - B = 100100111010`