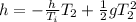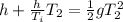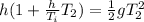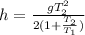Answer:
The height of the elevator at
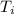 is
is
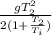
Solution:
As per the question:
Let us assume:
The velocity with which the elevator ascends be u'
The height attained by the elevator at time,
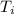 be h
be h
Thus
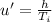 (1)_
(1)_
Now, with the help of eqn (2) of motion, we can write:

Using eqn (1):